Thomas Bayes (1702-1761)
"Given the number of times in which an unknown event has happened and failed: Required the chance that the probability of its happening in a single trial lies somewhere between any two degrees of probability that can be named."
In a (now) famous essay published posthumously (1764), Thomas Bayes asked this question, and gave an answer. The question is a version of "inverse problem":if you know that a certain kind of event E (e.g., head appears on a coin toss) occurs with probability x, you can calculate the probability that E occurs s times out of n trials, and this is a "direct problem"; but Bayes's question goes into the opposite direction, looking for the correct value of x (e.g., what's the probability of head on this coin?), based on the result of n trials, and hence it is "inverse".
First, it must be noticed that he defined probability as follows: The probability of any event is the ratio of the value at which an expectation depending on the happening of the event ought to be computed, and the value of the thing expected upon its happening. In short, he regarded probability as a sort of (rational) betting ratio, and he tried to derive the laws of probability (including what we now call Bayes's Theorem) from this definition. Thus it is quite understandable why modern Bayesians call themselves by his name.
Getting back to the initial question: Bayes obtained a solution by means of an ingenious geometrical representation of the problem. It is important to understand why Bayes needed such a geometrical representation. He defined probability as a betting ratio, so that a probability must be assigned to an event (or proposition, for that matter) which either occurs (true) or does not occur (false); otherwise a bet does not make sense! Thus, instead of speaking of "the correct value x lies between y and z", he had to talk about a concrete event, either coming true or not coming true.
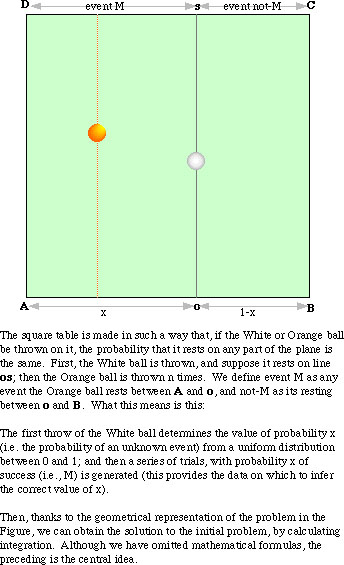
With the above figure in mind, it should be clear that the probability of "an unknown event M" can be expressed by
P(M) = x,
and the calculation of the probability of any compound event (a series of events) can be carried out by employing the laws of probability. In particular, the probability that the White ball comes to rest between stated limits (say, between y and z), given the number of M and not-M in n trials of the Orange ball (let K signify this information), can be represented by
P(yüģxüģz, K)
and we can obtain the solution by integration. But notice that this solution assumes a uniform distribution of prior probability over the possible values of x.
The personal life of Bayes is scarcely known. He was a nonconformist preacher (Presbyterian), and a Fellow of the Royal Society.
ü@
References
[There are many papers on Bayes, and I mention only two recent works which are quite useful; they have a good bibliography.]
Bayes, Thomas (1764) "An Essay towards Solving a Problem in the Doctrine of Chances", Philosophical Transactions of the Royal Society of London 53.
Dale, A. I. (1999) A History of Inverse Probability, 2nd ed., Springer, 1999, chh. 2-4.
Earman, J. (1992) Bayes or Bust? MIT Press, 1992, ch. 1.