Hermann Minkowski was born in Russia, and educated in Germany. He was one of Einstein's teachers at Zuerich, and later invented "Minkowski Space" for expressing Einstein's theory of special relativity. He joined the Mathematics Department of Goettingen and became one of the close colleagues of David Hilbert there in 1902.
The beginning part of his address delivered at the 80th Assembly of German Natural Scientists and Physicians (September 21, 1908) is now famous:
That is his four-dimensional space where time and 3-space intermingle, and the Lorentz Geometry of spacial relativity can be nicely represented. This nice representation certaily helped Einstein's quest for general relativity.The views of space and time which I wish to lay before you have aprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.
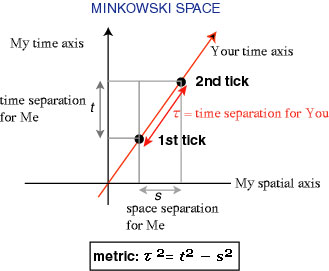
Although some people still follow Einstein's misleading terminology that a Minkowski space is Euclidean in a way, this writer would recommend the following terminology instead: The spacetime geometry expressed by a Minkowski space should be called the "Lorentz Geometry", since its crucial metric is Lorentzian, in that it produces the invariance with respect to the Lorentz transformation. Moreover, the Pythagorean Theorem does not hold in a Minkowski space, because the time part and the spatial part have a different sign. Suppose you move uniformly relative to me, carrying a standard clock. Then your time interval (proper time) is related with my space and time as in the following figure, and it is clear that the Pythagorean Theorem does not hold:
BACK TO MINKOWSKI PICTURE//BACK TO GALLERY INDEX