|
|
|
科学哲学ニューズレター |
![]()
No. 56, November 5, 2004
Einstein and the Philosophy of Space and Time, by Soshichi Uchii
Editor: Soshichi Uchii
以下の文章は、ミネルヴァ書房から12月に出る予定になっている最新著『アインシュタインの思考をたどる──時空の哲学入門』、第4章までの概要をPR誌のために書き下ろしたものである。厳しい字数制限のもとで書かれた原稿なので、よりよい理解のために必要と思われる補足や図を注で付け加えておく。Spacetime 2004 参照。
アインシュタインと時空の哲学、内井惣七
1. 同時性の相対性
2005年は相対性理論が発表されてからちょうど百周年となる。「運動する物体の電気力学」という1905年の論文で、アインシュタインは「相対性原理」と「光速度一定の原理」という二原理を要請し、これらを認めると、当時の多くの物理学者が頭を悩ませていた力学と電磁気学との間の不調和が消えてなくなることを示したのだった。この理論は特殊相対性理論と呼ばれる。このようにして、アインシュタインは二十世紀の物理学における変革を先頭切って始めた。続いて、1907年から新しい重力理論を構築し始め、その成果は1915年の一般相対性理論となって完成する。これら二つの相対性理論によってもたらされた、空間と時間の哲学における概念的変革は、いまだに人々に理解されにくい。
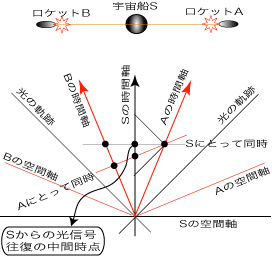
ニュートンの力学では、遠く離れた二つの場所でそれぞれ出来事が生じても、それら二つの出来事が同時に生じたかどうかは、宇宙の中のどこにおいても同じペースで流れている絶対時間によって簡単に決まる仕掛けになっていた。しかし、アインシュタインが要請した光速度一定の原理によれば、たとえば一定速度で直進する宇宙船Sと、Sに相対的に右へ光速の1/2で直進するロケットA、左へ光速の1/2で直進するロケットBがあったとき(図1参照)、どれから見ても、光速は同じである。右に進行するロケットから宇宙船に向けて発射された光は、当のロケットから見ても、宇宙船から見ても、左に進行するロケットから見ても等しい早さで進行する。ふつうの人の常識では「そんなアホな!」ということになろう。しかし、それは宇宙船やロケットの運動状態によらず通用する同時性の基準があって、共通の時間が流れていると想定したからなのである。これが絶対時間の正体だったのだ。
これに対し、相対性理論によれば、光はこの宇宙で最速の信号であり、いかなる信号もこれより早く伝わることはない。そこで、アインシュタインによる同時性の基準は、この有限速度の光信号を使って組み直される。宇宙船と右行きのロケットに考察を絞ろう。アインシュタインの新しい定義によれば、宇宙船Sから発射した光がロケットAで反射して戻ってきたとき、Sの時計による経過時間の半分の時点に光はAに到着したとみなす。つまり、光がAに到着したという出来事と、Sの時計が先の時点を指した出来事はSにとって同時である、と定義される。この定義において、右向きの光線と左向きの光線は速度が等しいと規約によって決めるのである。もちろん、ロケットにとっての同時性も同じようにして(ただし、ロケットの時計で時間を計る)それぞれ定義される。こういった定義と、特殊相対性の特質をもっとも簡明に表現する手段として、「ミンコフスキ時空」にまさるものはない(図1参照)。
図1 三つの系のミンコフスキ時空
このように定義された「同時性」によれば、Sにとって同時な出来事と、ロケットAにとって同時な出来事とは異なってくる。これが「同時性の相対性」にほかならない。Aにとっての時空は、Sにとっての時空に対して図のように傾いているのである。
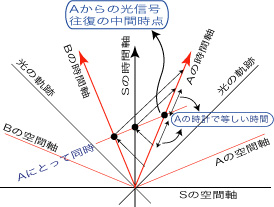
注) Aにとっての同時性は、次図のようにして決まる。Aから光信号をSおよびBに向けて発射し、反射して帰ってきた時間をAの時計で計って、経過時間の半分の時点を求める。この時点がそれぞれの系で光信号が反射した出来事と同時である。
2.等価原理から曲がった時空へ
アインシュタインの重力理論は、1907年の「わが生涯のもっともすばらしい考え」から始まる。「等価原理」と呼ばれるこの着想は、加速運動と重力場の存在とが物理的に同等だという内容のもの。きわめて乱暴な言い方をすれば、車の急発進、急ブレーキのたびに、運転者は周りに重力場を作り出しているということになろうか。特殊相対性理論で加速運動は扱えるので、この発想をテコにして重力の扱いに突破口が開けたわけである。同時に、「重力」という言葉に、アインシュタインは思いもかけなかった広い意味を新たに与えたということにもなる。そして、彼は1907年の論文で、重力場がもたらす新しい効果を発見した。太陽や地球など、重力場の源となる物体の近くにある時計と遠くにある時計とを比べたとき、同じ作りであるにもかかわらず、近くの時計のほうがペースが遅くなるのである。これは、いわば、重力によって時間が曲がるということに相当する。それだけではなく、光線は重力場を生み出す物体のほうへ巻き付くように曲がるという予測も導き出された。
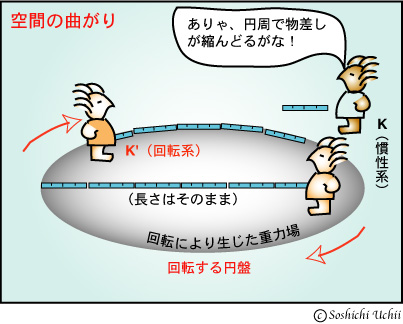
しかし、このような画期的な予言をもたらした発想も、1912年頃には限界に達し、もう一段の飛躍を必要とすることになる。アインシュタインは、重力場の中では時間だけでなく空間も曲がることに気づいたのである。これは、回転する円盤の考察に基づく。回転する円盤において遠心力が働くことは、日常経験からも明らかである。しかし、アインシュタインの拡張された重力概念によれば、遠心力の発生は重力場の発生と同じである。このとき、円周上に物差しを並べてみれば、それらは一定の速度で運動することになるから、傍観者から見れば(特殊相対性理論により)長さが縮んで見える。しかし、直径方向ではこういった運動はないので、物差しの長さは同じままに見える(図2参照)。とすると、円周方向には縮んだ物差しが静止していた円盤においてよりもたくさん並んで、円周率がπより大きくなる。つまり、ユークリッド幾何学が成り立たないのである(特殊相対性理論を適用するには、物質的な拘束力の働いている円盤そのものではなく、拘束から自由な物差しを考えなければならないことに注意)。
図2 回転系の空間
かくして、特殊相対性理論と等価原理だけではどうにもならなくなって、曲がった時空を扱えるような数学、非ユークリッド幾何学が必要になってくる。そして、自由に曲がった座標系を採用してもよいような重力理論が構想されたのである。もちろん、どのような座標系を採用しても、表現される重力法則は同じでなければならない。つまり、座標系を曲げていけば、時空の間隔や法則の表現も連動して変化しなければならない。これが、専門用語では「一般共変性」と呼ばれる条件にほかならない。そこで、アインシュタインはこれを扱えるような数学、微分幾何学を、旧友グロスマンの助けを得て猛勉強し、一般共変性を満たす重力場方程式を目指した。
3.落とし穴とそこからの脱出
アインシュタインとグロスマンは1913年に重力についての共著論文を発表した。これは後の一般相対性理論に向けての、いわば中間報告だったのだが、大きな進展とともに、予想外の大きな難点も含まれているものだった。一般共変な重力場方程式に向けて、ほとんどの道具立ては立派にそろっていたのだが、肝心の方程式が一般共変性を満たす形に書けなかったのだった。その一因は、回転しない星の周りのような、時間的に変動しない重力場に関するアインシュタインの思い違いにあったらしい。静的重力場で空間は曲がっていないと彼は誤って仮定したのだった。しかも、悪いことに、その後アインシュタインは重力場の方程式が一般共変性を満たすことは不可能だという「証明」を得たと思いこんだ。この「証明」は、「穴の議論」と名付けられて、近年欧米で盛んに論じられている。詳細はここでは述べられないが、要するに、一般共変な方程式の解は、同じ座標系内でも複数ありうるので重力場の一義性が保証されないとアインシュタインは考えたのである。この思いこみから脱却するために、アインシュタインは二年を費やしてしまったらしい。
アインシュタインの重力理論は、何しろ史上初めて一般共変性を満たすような形式で書かれたものだったので、アインシュタインはその数学的特性を理解するために、既成の概念的束縛を打破する必要があった。実際、物理的には同一の解が、数学的には異なる複数の表現をとって現れるという事態は、彼の重力場の方程式で初めてあらわになった特異性である。アインシュタインは、数学的な一義性と物理的な一義性を区別し、肝心なのは後者であるという認識を得てこの苦境を脱出した。同時に、数学的な座標系を設定することと、物理的時空を記述することの間には大きなギャップがあることも認識した。簡単に言えば、座標系を設定しただけでは物理的時空は何も記述されておらず、重力場方程式の解として得られるメトリック(計量)が伴ってはじめて物理的時空が記述できるのである。この認識にたどり着いたのが1915年の秋に入る頃らしい。
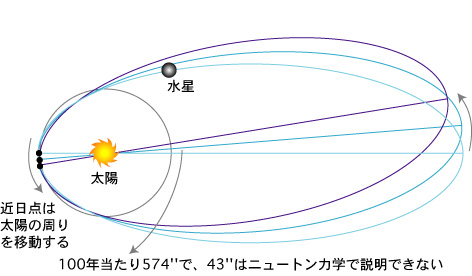
この落とし穴を克服すれば、あとは一気呵成となる。1915年の11月に入り、アインシュタインは毎週プロイセン・アカデミーで論文を発表し、11月18日には水星の近日点移動の謎を解くというハイライトがくる(図3参照)。ニュートン力学で謎だった43秒の余分な移動は、一般相対性理論でピタリと解決できたのである。同時に、近似解を通じてではあるが、静的重力場でも空間が曲がるので、星の周りでの光の湾曲も、四年前の予測に比べて二倍になることを悟るのである。こうして、11月25日、ついに重力場の方程式が完成した。
図3 水星の近日点移動
こうして完成した一般相対性理論も、その内容が本当に理解され始めるのは、実に1960年代以後となる。星の重力崩壊やブラックホールの可能性が真剣に検討され始める段になって、アインシュタインの重力理論が内包していたとてつもない可能性がだんだんと明らかにされてきたのである。
November 7 , 2004. (c) Soshichi Uchii